Symmetrie: Unterschied zwischen den Versionen
K (Ziko van Dijk verschob Seite Entwurf:Symmetrie nach Symmetrie) |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (19 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[ | [[Datei:Eastern Tiger Swallowtail Papilio glaucus on Milkweed 2800px.jpg|thumb|Dieser Schwalbenschwanz-Schmetterling kann seine [[Flügel]] genau aufeinanderlegen, weil sie achsen-symmetrisch sind.]] | ||
Wer sich vor einen Spiegel stellt, sieht darin seinen eigenen [[Körper]]. Das Original und das Spiegelbild nennt man spiegelverkehrt oder symmetrisch. Jeder Gegenstand bildet in einem Spiegel ein symmetrisches Abbild. | Wer sich vor einen Spiegel stellt, sieht darin seinen eigenen [[Körper]]. Das Original und das Spiegelbild nennt man spiegelverkehrt oder symmetrisch. Jeder Gegenstand bildet in einem Spiegel ein symmetrisches Abbild. | ||
Der [[Mensch]] an sich ist auch bereits eine symmetrische Figur. Die linke Seite steht spiegelverkehrt zur rechten Seite. Dies stimmt | Der [[Mensch]] an sich ist auch bereits eine symmetrische Figur. Die linke Seite steht spiegelverkehrt zur rechten Seite. Dies stimmt nicht ganz: Ein Gesicht ist meistens ein wenig einseitig. Grob gesehen kann man trotzdem sagen, dass ein Gesicht symmetrisch ist. | ||
Bei einigen [[ | Bei einigen [[Tiere]]n ist die Symmetrie ganz offensichtlich, zum Beispiel beim Schmetterling. Auf einem [[Foto]] könnte man eine [[Linie]] finden, welche den Schmetterling in zwei gleiche Hälften teilt. An dieser [[Linie]] könnte man das [[Papier]] falten, sodass beide Hälfte der Figur genau aufeinanderpassen. Man nennt sie deshalb deckungsgleich. Die Faltlinie heißt Symmetrieachse. | ||
Viele technische Dinge, zum Beispiel [[Flugzeug]]e, sind nahezu perfekt achsensymmetrisch. Wäre ein Flugzeug nicht achsensymmetrisch, so könnte es nicht richtig fliegen. Es gibt auch [[Haus|Wohnhäuser]] oder [[Schloss|Schlösser]], die genau achsensymmetrisch gebaut sind. | Viele technische Dinge, zum Beispiel [[Flugzeug]]e, sind nahezu perfekt achsensymmetrisch. Wäre ein Flugzeug nicht achsensymmetrisch, so könnte es nicht richtig fliegen. Es gibt auch [[Haus|Wohnhäuser]] oder [[Schloss|Schlösser]], die genau achsensymmetrisch gebaut sind. | ||
== Gibt es noch andere Arten von Symmetrien? == | == Gibt es noch andere Arten von Symmetrien? == | ||
Einige Figuren kann man drehen, und in bestimmten Stellungen sehen sie immer wieder gleich aus. Das beste Beispiel ist das Windrad. Man kann es um einen Flügel weiterdrehen, ohne dass man einen Unterschied erkennt. Die Bilder sind also deckungsgleich. Man nennt dies Drehsymmetrie. | Einige Figuren kann man drehen, und in bestimmten Stellungen sehen sie immer wieder gleich aus. Das beste Beispiel ist das [[Windrad]]. Man kann es um einen [[Flügel]] weiterdrehen, ohne dass man einen Unterschied erkennt. Die Bilder sind also deckungsgleich. Man nennt dies Drehsymmetrie. | ||
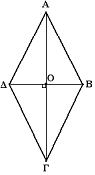
Es gibt auch punktsymmetrische Figuren, zum Beispiel den Rhombus. Man kann ihn an seinem Mittelpunkt spiegeln. So sieht er wieder genau gleich aus. | Es gibt auch punktsymmetrische Figuren, zum Beispiel den Rhombus. Man kann ihn an seinem Mittelpunkt spiegeln. So sieht er wieder genau gleich aus. | ||
| Zeile 16: | Zeile 16: | ||
<gallery> | <gallery> | ||
Datei:Lazienki Palace reflected at night (26398586470).jpg|Dieser [[Schloss|Palast]] in [[Warschau]] ist genau achsen-symmetrisch. | |||
Datei:2010-05-11-Windspiel.JPG|Dieses Windspiel ist drehsymmetrisch und punktsymmetrisch. | |||
Datei:CH-Windrad.jpg|Dieses Windspiel ist drehsymmetrisch, aber nicht punktsymmetrisch. | |||
Datei:13 K di cuori.jpg|Der [[König]] auf dieser Spielkarte ist ebenfalls drehsymetrisch. | |||
Datei:Rhombus (1).png|Diesen Rhombus kann man nicht nur an seinen Diagonalen, sondern auch an seinem Mittelpunkt spiegeln. Das ist eine Punktsymmetrie. | |||
</gallery> | </gallery> | ||
{{Artikel|mini=ja}} | |||
[[Kategorie: | [[Kategorie:Wissenschaft und Technik]] | ||
Aktuelle Version vom 22. Juni 2024, 17:59 Uhr
Wer sich vor einen Spiegel stellt, sieht darin seinen eigenen Körper. Das Original und das Spiegelbild nennt man spiegelverkehrt oder symmetrisch. Jeder Gegenstand bildet in einem Spiegel ein symmetrisches Abbild.
Der Mensch an sich ist auch bereits eine symmetrische Figur. Die linke Seite steht spiegelverkehrt zur rechten Seite. Dies stimmt nicht ganz: Ein Gesicht ist meistens ein wenig einseitig. Grob gesehen kann man trotzdem sagen, dass ein Gesicht symmetrisch ist.
Bei einigen Tieren ist die Symmetrie ganz offensichtlich, zum Beispiel beim Schmetterling. Auf einem Foto könnte man eine Linie finden, welche den Schmetterling in zwei gleiche Hälften teilt. An dieser Linie könnte man das Papier falten, sodass beide Hälfte der Figur genau aufeinanderpassen. Man nennt sie deshalb deckungsgleich. Die Faltlinie heißt Symmetrieachse.
Viele technische Dinge, zum Beispiel Flugzeuge, sind nahezu perfekt achsensymmetrisch. Wäre ein Flugzeug nicht achsensymmetrisch, so könnte es nicht richtig fliegen. Es gibt auch Wohnhäuser oder Schlösser, die genau achsensymmetrisch gebaut sind.
Gibt es noch andere Arten von Symmetrien?
Einige Figuren kann man drehen, und in bestimmten Stellungen sehen sie immer wieder gleich aus. Das beste Beispiel ist das Windrad. Man kann es um einen Flügel weiterdrehen, ohne dass man einen Unterschied erkennt. Die Bilder sind also deckungsgleich. Man nennt dies Drehsymmetrie.
Es gibt auch punktsymmetrische Figuren, zum Beispiel den Rhombus. Man kann ihn an seinem Mittelpunkt spiegeln. So sieht er wieder genau gleich aus.
Spielkarten sind besonders interessant. Einige sind achsensymmetrisch. Andere sind drehsymmetrisch und gleichzeitig punktsymmetrisch. Am besten probiert man es selber aus.
Dieses Windspiel ist drehsymmetrisch und punktsymmetrisch.
Dieses Windspiel ist drehsymmetrisch, aber nicht punktsymmetrisch.
Der König auf dieser Spielkarte ist ebenfalls drehsymetrisch.
Diesen Rhombus kann man nicht nur an seinen Diagonalen, sondern auch an seinem Mittelpunkt spiegeln. Das ist eine Punktsymmetrie.
.jpg)
.png)
Klexikon.de ist die Wikipedia für Kinder zwischen 5 und 15 Jahren, also ein kostenloses Online-Lexikon für Schulkinder. Zum Thema Symmetrie findet ihr einen besonders einfachen Artikel auf MiniKlexikon.de und weitere Kinderseiten in der Kindersuchmaschine „Frag Finn“.
Das Klexikon wird gefördert durch den weltgrößten Wikipedia-Förderverein Wikimedia Deutschland, die Beauftragte der Bundesregierung für Kultur und Medien, die Bundeszentrale für Kinder- und Jugendmedienschutz und die Medienanstalt Berlin-Brandenburg.
Unsere Klexikon-Botschafter sind die KiKA-Moderatoren Ralph Caspers („Wissen macht Ah!“, “Die Sendung mit der Maus“ und „Frag doch mal die Maus“) und Julian Janssen („Checker Julian“).
Das Kinderlexikon Klexikon sorgt für Medienkompetenz und Bildungsgerechtigkeit und ist wie die Wikipedia auf Spenden angewiesen. Denn hier finden Schülerinnen und Schüler zu 3.500 Themen das Wichtigste einfach erklärt, mit Definition und Bildern. Das ist Grundwissen kindgerecht und leicht verständlich für Unterricht, Hausaufgaben und Präsentationen in der Schule.
