|
|
| (26 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| == Symmetrie ==
| | [[Datei:Eastern Tiger Swallowtail Papilio glaucus on Milkweed 2800px.jpg|thumb|Dieser Schwalbenschwanz-Schmetterling kann seine [[Flügel]] genau aufeinanderlegen, weil sie achsen-symmetrisch sind.]] |
| Mit dem Begriff Symmetrie bezeichnet man die Handlung, mit der ein Objekt, zum Beispiel durch Bewegungen wie einer Spiegelung, Drehung oder Verschiebung, auf sich selbst abgebildet werden kann, also unverändert erscheint. Gelingt dies, so nennt man dieses Objekt symmetrisch. Symmetrisch sein können eindimensionale, zweidimensionale oder dreidimensionale Objekte.
| | Wer sich vor einen Spiegel stellt, sieht darin seinen eigenen [[Körper]]. Das Original und das Spiegelbild nennt man spiegelverkehrt oder symmetrisch. Jeder Gegenstand bildet in einem Spiegel ein symmetrisches Abbild. |
| Manchmal werden auch zwei (oder mehrere) verschiedene Objekte als zueinander symmetrisch bezeichnet, wenn sie, zusammen betrachtet, eine symmetrische Figur bilden.
| |
|
| |
|
| == Was ist Achsensymmetrie? ==
| | Der [[Mensch]] an sich ist auch bereits eine symmetrische Figur. Die linke Seite steht spiegelverkehrt zur rechten Seite. Dies stimmt nicht ganz: Ein Gesicht ist meistens ein wenig einseitig. Grob gesehen kann man trotzdem sagen, dass ein Gesicht symmetrisch ist. |
| Die Achsensymmetrie ist eine Form der Symmetrie. Oft wird sie auch Spiegelsymmetrie genannt. Jedes Objekt, das an einer Achse gespiegelt wird, bildet mit seinem erzeugten Spiegelbild eine achsensymmetrische Figur. Der Spiegel ist in diesem Fall die Symmetrieachse.
| |
| Es gibt aber auch Figuren, die bereits in sich achsensymmetrisch sind. Dann findet man in dieser Figur mindestens eine Symmetrieachse.
| |
| Würde man diese achsensymmetrische Figur auf ein Blatt Papier malen, ließe sich eine Linie finden, die die Figur in zwei gleiche Hälften teilt. An dieser Linie (Symmetrieachse) könnte man das Papier falten, sodass beide Hälfte der Figur genau aufeinander passen – sie sind also deckungsgleich.
| |
|
| |
|
| Beispiele für die Achsensymmetrie sind in der Umwelt überall zu finden. Sieht man sich in der Natur beispielsweise einen Schmetterling an, so erscheinen beide Flügel achsensymmetrisch. Auch wir Menschen sehen auf den ersten Blick achsensymmetrisch aus: Alles, was es links gibt, gibt es auch rechts (Augen, Arme, Beine,...). Aber wenn man ganz genau hinsieht, bemerkt man, dass wir nicht perfekt achsensymmetrisch sind. Alleine schon an den Händen kann man Unterschiede feststellen. In der Natur gibt es also nur Beispiele für die Achsensymmetrie, die aber nicht mathematisch exakt achsensymmetrisch sind.
| | Bei einigen [[Tiere]]n ist die Symmetrie ganz offensichtlich, zum Beispiel beim Schmetterling. Auf einem [[Foto]] könnte man eine [[Linie]] finden, welche den Schmetterling in zwei gleiche Hälften teilt. An dieser [[Linie]] könnte man das [[Papier]] falten, sodass beide Hälfte der Figur genau aufeinanderpassen. Man nennt sie deshalb deckungsgleich. Die Faltlinie heißt Symmetrieachse. |
|
| |
|
| Andere Objekte in unserer Umwelt zum Beispiel im Bereich der Technik, wie das Flugzeug, bieten eine nahezu perfekte Achsensymmetrie an. Wäre ein Flugzeug nicht achsensymmetrisch, so könnte es nicht richtig fliegen. Auch das Schaukeln macht mehr Spaß, wenn die Schaukel achsensymmetrisch aufgehängt ist, sonst würde man ganz schief auf dem Brettchen sitzen.
| | Viele technische Dinge, zum Beispiel [[Flugzeug]]e, sind nahezu perfekt achsensymmetrisch. Wäre ein Flugzeug nicht achsensymmetrisch, so könnte es nicht richtig fliegen. Es gibt auch [[Haus|Wohnhäuser]] oder [[Schloss|Schlösser]], die genau achsensymmetrisch gebaut sind. |
|
| |
|
| In der Mathematik findet man die vollkommene Achsensymmetrie: Man erkennt sie daran, dass jeder Punkt der Figur links und rechts von der Symmetrieachse immer denselben Abstand hat. Ein Rechteck hat zum Beispiel genau zwei Symmetrieachsen. Im Gegensatz dazu hat der Kreis unendlich viele Symmetrieachsen, man könnte also noch viel mehr pinke Symmetrieachsen in das Bild einzeichnen.
| | == Gibt es noch andere Arten von Symmetrien? == |
| | Einige Figuren kann man drehen, und in bestimmten Stellungen sehen sie immer wieder gleich aus. Das beste Beispiel ist das [[Windrad]]. Man kann es um einen [[Flügel]] weiterdrehen, ohne dass man einen Unterschied erkennt. Die Bilder sind also deckungsgleich. Man nennt dies Drehsymmetrie. |
|
| |
|
| Auch Palindrome, als besondere Muster in der Arithmetik, können achsensymmetrisch sein. Ein solches Palindrom ist zum Beispiel die Zahl 88088. In diesem Palindrom findet man zwei Symmetrieachsen. Dies liegt daran, dass jede Ziffer in sich sowohl eine vertikale, als auch horizontale Symmetrieachse hat.
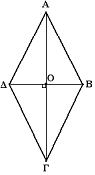
| | Es gibt auch punktsymmetrische Figuren, zum Beispiel den Rhombus. Man kann ihn an seinem Mittelpunkt spiegeln. So sieht er wieder genau gleich aus. |
|
| |
|
| == Drehsymmetrie ==
| | Spielkarten sind besonders interessant. Einige sind achsensymmetrisch. Andere sind drehsymmetrisch und gleichzeitig punktsymmetrisch. Am besten probiert man es selber aus. |
|
| |
|
| Die Drehsymmetrie ist eine Form der Symmetrie.
| | <gallery> |
| Hier wird eine Figur um einen Punkt gedreht. Der Punkt, um den man die Figur dreht, heißt Z. Der Punkt Z kann innerhalb oder außerhalb der Figur liegen.
| | Datei:Lazienki Palace reflected at night (26398586470).jpg|Dieser [[Schloss|Palast]] in [[Warschau]] ist genau achsen-symmetrisch. |
| Man nennt diesen Punkt Z auch Symmetriezentrum.
| | Datei:2010-05-11-Windspiel.JPG|Dieses Windspiel ist drehsymmetrisch und punktsymmetrisch. |
| | | Datei:CH-Windrad.jpg|Dieses Windspiel ist drehsymmetrisch, aber nicht punktsymmetrisch. |
| Man kann eine drehsymmetrische Figur zwischen 0 und 360 Grad drehen. Man muss beachten, dass die Drehung unter 360 Grad (das ist eine ganze Drehung) liegt. Dabei ist wichtig, dass die Figur nach der Drehung genauso aussieht wie vorher. Man sagt, die Figur kommt mit sich selbst zur Deckung. Das bedeutet, dass die Figur deckungsgleich ist.
| | Datei:13 K di cuori.jpg|Der [[König]] auf dieser Spielkarte ist ebenfalls drehsymetrisch. |
| Klassischerweise wird eine Figur entgegen den Uhrzeigersinn, also links herum, gedreht.
| | Datei:Rhombus (1).png|Diesen Rhombus kann man nicht nur an seinen Diagonalen, sondern auch an seinem Mittelpunkt spiegeln. Das ist eine Punktsymmetrie. |
| | | </gallery> |
| Die folgenden Bilder stellen eine drehsymmetrische Figur, nämlich ein Windrad, dar. Die acht Dreiecke des Windrades haben unterschiedliche Farben, damit man erkennen kann, dass sich die Figur dreht. Genau gleich sieht die Figur wegen der Farben nicht aus. Die Form verändert sich nach der Drehung aber nicht. Die Dreiecke kommen, um eine bestimmte Gradzahl oder einen bestimmten Teil einer ganzen Drehung gedreht miteinander zur Deckung. Das hellblaue Dreieck wandert einmal gegen den Uhrzeigersinn im Kreis herum und nimmt dabei nacheinander den Platz eines anderen Dreiecks ein.
| | {{Artikel|mini=ja}} |
| Das Drehzentrum ist dabei das schwarze Kreuz in der Mitte der Figur. Da, wo sich die Spitzen aller Dreiecke treffen.
| | [[Kategorie:Wissenschaft und Technik]] |
| | |
| | |
|
| |
| | |
| | |
| Allerdings kann nicht jede Figur um jede Gradzahl gedreht werden.
| |
| 360°, also eine ganze Drehung funktioniert bei jeder Figur.
| |
| Deswegen muss die Drehung bei einer drehsymmetrischen Figur auch kleiner als 360° (weniger als eine ganze Drehung) sein.
| |
| Beim Beispiel unserer Windmühle oben gibt es sieben Möglichkeiten, die Figur zu drehen, ohne dass sich die Form verändert. Darunter auch 180°(eine halbe Drehung). Somit ist die Windmühle auch
| |
| punktsymmetrisch. Wenn man nun andere Gradzahlen ausprobiert, kann man sehen, dass die einzelnen Dreiecke nicht miteinander zur Deckung kommen. | |
|
| |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| == Punktsymmetrie ==
| |
| | |
| Eine besondere Form der Drehsymmetrie ist die Punktsymmetrie, beziehungsweise Halbdrehung. Punktsymmetrische Figuren erkennt man daran, dass sie bei einer halben Drehung, also einer Drehung um 180 Grad, wieder auf sich selbst abgebildet werden. Sie sehen trotz der Drehung unverändert aus.
| |
| | |
| Das kann man gut am Beispiel einer Spielkarte zeigen:
| |
|
| |
| Spielkarten bestehen aus zwei Hälften. Dreht man die eine Hälfte der Karte um 180 Grad, so wird sie exakt auf die andere Hälfte abgebildet. Das bedeutet, dass die beiden Hälften einer Spielkarte punktsymmetrisch zueinander sind. Gedreht wird dabei um einen Drehpunkt Z, der genau in der Mitte der Begrenzungslinie zwischen den beiden Kartenhälften liegt. Diesen Drehpunkt nennt man auch das Symmetriezentrum bei einer Punktspiegelung. (Dieser Punkt wurde durch ein rotes Kreuz markiert).
| |
| | |
| Statt einer halben Drehung um den Drehpunkt Z kann man eine punktsymmetrische Figur auch durch die Spiegelung der Figur an einem Punkt herstellen. Dieser Punkt ist identisch dem Drehpunkt Z. Bezogen auf unser Beispiel der Spielkarte bedeutet das, dass jeder Punkt der einen Kartenhälfte an dem blau markierten Symmetriezentrum zwischen den beiden Kartenhälften gespiegelt wird. Und zwar so:
| |
| | |
| Nehmen wir als Beispiel die abgebildete Rose auf der oberen Bildhälfte:
| |
| | |
| # Nummerierter Listeneintrag
| |
| 1. Nimm dein Geodreieck zur Hilfe und lege es mit dem 0- Punkt an dem Symmetriezentrum Z an.
| |
| 2. Zeichne eine Verbindunglinie von der Rose zum Symmetriezentrum Z.
| |
| 3. Verlängere diese Linie auf der anderen Seite von Z um den gleichen Abstand. So erhältst du als Bildpunkt der Rose auf der oberen Bildhälfte genau denselben Punkt auf der unteren Bildhälfte.
| |
| Ebenso könnte man mit allen anderen Punkten der oberen Kartenhälfte vorgehen und so die entsprechenden Bildpunkte auf der unteren Kartenhälfte ermitteln.
| |
| | |
| Eine Punktspiegelung einer Figur an dem Punkt Z führt also zu dem gleichen Ergebnis wie eine Drehung der Figur um 180° um den Punkt Z. Der Punkt Z liegt dabei im Symmetriezentrum der punktsymmetrischen Figur. Das Symmetriezentrum ist der Punkt, von dem aus man eine Gerade von einem Punkt zu seinem Bildpunkt ziehen kann. Bezogen auf unser Beispiel mit der Spielfigur zum Beispiel von der Nasenspitze auf der oberen Bildhälfte zur Nasenspitze auf der unteren Bildhälfte, von dem einen Mund zu dem anderen oder von einer Schleife zu der anderen. Dort wo sich alle diese Verbindungsgeraden von Punkt zu Bildpunkt schneiden liegt das Symmetriezentrum und damit der Punkt Z. (In unserem Beispiel mit der Spielkarte war es die Mitte der beiden Kartenhälften).
| |
| | |
| Eigenschaften der Punktsymmetrie/ Halbdrehung sind, dass sie eine besondere Form der Drehsymmetrie ist, nämlich eine Drehung um 180°. Außerdem sind Original- und Bildfigur (in unserem Beispiel obere und untere Kartenhälfte) bei einer punktsymmetrischen Figur zueinander deckungsgleich sind. Das bedeutet, dass beide Figuren die gleiche Form und die gleiche Größe besitzen.
| |
| | |
| Neben Spielkarten lassen sich natürlich noch viele andere punktsymmetrische Figuren und auch Buchstaben. Bei den folgenden ist das Symmetriezentrum jeweils durch ein blaues Kreuz markiert:
| |
Wer sich vor einen Spiegel stellt, sieht darin seinen eigenen Körper. Das Original und das Spiegelbild nennt man spiegelverkehrt oder symmetrisch. Jeder Gegenstand bildet in einem Spiegel ein symmetrisches Abbild.
Der Mensch an sich ist auch bereits eine symmetrische Figur. Die linke Seite steht spiegelverkehrt zur rechten Seite. Dies stimmt nicht ganz: Ein Gesicht ist meistens ein wenig einseitig. Grob gesehen kann man trotzdem sagen, dass ein Gesicht symmetrisch ist.
Bei einigen Tieren ist die Symmetrie ganz offensichtlich, zum Beispiel beim Schmetterling. Auf einem Foto könnte man eine Linie finden, welche den Schmetterling in zwei gleiche Hälften teilt. An dieser Linie könnte man das Papier falten, sodass beide Hälfte der Figur genau aufeinanderpassen. Man nennt sie deshalb deckungsgleich. Die Faltlinie heißt Symmetrieachse.
Viele technische Dinge, zum Beispiel Flugzeuge, sind nahezu perfekt achsensymmetrisch. Wäre ein Flugzeug nicht achsensymmetrisch, so könnte es nicht richtig fliegen. Es gibt auch Wohnhäuser oder Schlösser, die genau achsensymmetrisch gebaut sind.
Gibt es noch andere Arten von Symmetrien?
Einige Figuren kann man drehen, und in bestimmten Stellungen sehen sie immer wieder gleich aus. Das beste Beispiel ist das Windrad. Man kann es um einen Flügel weiterdrehen, ohne dass man einen Unterschied erkennt. Die Bilder sind also deckungsgleich. Man nennt dies Drehsymmetrie.
Es gibt auch punktsymmetrische Figuren, zum Beispiel den Rhombus. Man kann ihn an seinem Mittelpunkt spiegeln. So sieht er wieder genau gleich aus.
Spielkarten sind besonders interessant. Einige sind achsensymmetrisch. Andere sind drehsymmetrisch und gleichzeitig punktsymmetrisch. Am besten probiert man es selber aus.
Dieses Windspiel ist drehsymmetrisch und punktsymmetrisch.
Dieses Windspiel ist drehsymmetrisch, aber nicht punktsymmetrisch.
Der König auf dieser Spielkarte ist ebenfalls drehsymetrisch.
Diesen Rhombus kann man nicht nur an seinen Diagonalen, sondern auch an seinem Mittelpunkt spiegeln. Das ist eine Punktsymmetrie.