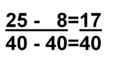Bruchrechnung

Die Bruchrechnung gehört in der Mathematik zum Themengebiet der Arithmetik.

Brüche beschreiben Anteile eines Ganzen.

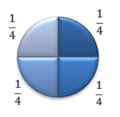
Zum Beispiel lassen sich Brüche anhand eines ganzen Kuchens veranschaulichen.

Wenn man den Kuchen in 4 gleich große Teile teilt, weil insgesamt vier Personen Kuchen essen wollen. So erhält jede Person ein Stück von

dem Kuchen, also ein Viertel des Kuchens. 

• 

  Ganzer Kuchen mit 4 Vierteln

Im nächsten Schritt wird ein Viertel von dem Kuchen gegessen.

Nimmt man ein Viertel von dem ganzen Kuchen weg, also von vier Vierteln, so bleibt am Ende drei Viertel von dem Kuchen übrig. 

• 
• 

Die Darstellung von Brüchen beruht also darauf, dass sich ein Ganzes (in diesem Beispiel der Kuchen) noch unterteilen lässt (in diesem Beispiel in vier gleich große Teile).

Brüche allgemein

Scheibweise

Ein Bruch wird in der „Zähler-Bruchstrich-Nenner-Schreibweise“ geschrieben. Die Zahl unter dem Bruchstrich bezeichnet man als Nenner. Der Nenner zeigt an, in wie viele gleich große Teile das Ganze aufgeteilt wird (Beispiel Kuchen: in 4 Teile). Die Zahl über dem Bruchstrich nennt man Zähler. Der Zähler zeigt an, wie viele Teile von dem Ganzen noch übrig bzw. vorhanden sind. (Beispiel Kuchen: 3 Teile sind noch vorhanden)
Man kann einen Kuchen in 4 gleich große Teile zerlegen. Er lässt sich aber auch in 6,8,12,... Teile zerlegen. Trotzdem ändert sich die Größe des Kuchens nicht.

• 

2 Viertel gleich 4 Achtel

Bruchzahl und Brüche

Für jede Bruchzahl gibt es unendlich viele Brüche, die alle den gleichen Wert bzw. die gleiche Bedeutung haben. Von einer Bruchzahl zu der nächsten Bruchzahl gelangt man durch Erweitern und Kürzen (siehe unten). Dabei verändert sich der Wert der Bruchzahl nicht. Es handelt sich lediglich um eine andere Form der Darstellung.

Kürzen

Kürzen von Brüchen

Der Wert einer Bruchzahl ändert sich nicht, wenn man Zähler und Nenner mit derselben Zahl multipliziert, also den Bruch erweitert.

Zum Beispiel:

Der Wert ändert sich auch nicht, wenn man Zähler und Nenner mit derselben Zahl dividiert, also den Bruch kürzt.

Zum Beispiel:

Rechnen mit Brüchen

Addieren und Subtrahieren von Brüchen

Brüche gleichnamig machen

Damit man Brüche addieren und subtrahieren kann, müssen diese zunächst gleichnamig gemacht werden. Gleichnamig bedeutet, dass die Brüche denselben Nenner haben. Dafür müssen die Brüche so erweitert oder gekürzt werden, bis ihr Nenner gleich ist.

In dem Beispiel rechts wurden die Nenner durch Multiplizieren auf die Zahl 40 erweitert. Nachdem die Brüche gleichnamig gemacht wurden, addiert man die Zähler miteinander. Der Nenner bleibt gleich!
Beispiel:

• 

Auch bei der Subtraktion müssen beide Brüche zunächst gleichnamig gemacht werden. Anschließend werden die Zähler subtrahiert. Die Nenner bleiben gleich.
Beispiel:

• 

Multiplizieren von Brüchen

Beim Multiplizieren von Brüchen müssen sie nicht erst gleichnamig gemacht werden. Hierbei werden jeweils die Zähler miteinander multipliziert (Zähler mal Zähler) und die Nenner miteinander multipliziert (Nenner mal Nenner).
Beispiel:

• 

Dividieren von Brüchen

Beim Dividieren muss man folgende Regel beachten: Brüche werden dividiert, indem man mit dem Kehrwert des zweiten Bruchs multipliziert. Den Kehrwert eines Bruchs erhält man, indem man Zähler und Nenner miteinander vertauscht. So ist der Kehrwert von ⁶/₅ --> ⁵/₆
Beispiel für eine Division:

•